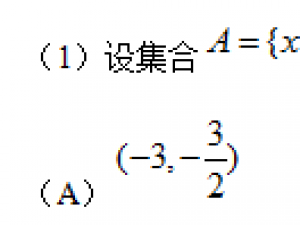《2016年重庆理科数学高考试题与参考答案(含解析)》是由大铁棍娱乐网(www.datiegun.com)编辑为你整理收集在【教育学习】栏目,于2016-06-12 13:56:40整理发布,希望对你有所帮助,可及时向我们反馈。
2016年重庆理科数学高考试题与参考答案(含解析),注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页.
2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置.
3.全部答案在答题卡上完成,答在本试题上无效.
4.考试结束后,将本试题和答题卡一并交回.

第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知z=(m+3+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是

(A){1}
(B){1,2}
(C){0,1,2,3,}
(D){-1,0,1,2,3}
【解析】C

解得m=8
故选D

故选A
(5)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为

(A)24(B)18(C)12(D)9
【解析】B
E---F有6种走法,F---G有3种走法,由乘法原理知,共6*3=18种走法
故选B.
(6)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为

(A)20π (B)24π (C)28π (D)32π
【解析】C
几何体是圆锥与圆柱的组合体,
设圆柱底面圆半径为r,周长为c,圆锥母线长为l,圆柱高为h.

故选C.

故选B.
(8)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=

(A)7(B)12(C)17(D)34
【解析】C
第一次运算:s=0*2+2=2,
第二次运算:s=2*2+2=6,
第三次运算:s=6*2+5=17,
故选C.

【解析】C
由题意得:(xi,yi)(i=1,2,…,n)在如图所示方格中,而平方和小于1的点均在
如图所示的阴影中


故选A.

第Ⅱ卷
本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.www.gaosan.com

【解析】②③④
(15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是
【解析】
![]()
由题意得:丙不拿(2,3),
若丙(1,2),则乙(2,3),甲(1,3)满足,
若丙(1,3),则乙(2,3),甲(1,2)不满足,
故甲(1,3),

三、解答题:解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)gaosan.con

(18)(本小题满分12分)
某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数01234
![]()
保 费0.85aa1.25a1.5a1.75a2a
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数01234
![]()
概 率0.300.150.200.200.100.05
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
【解析】 ⑴设续保人本年度的保费高于基本保费为事件A,

⑶解:设本年度所交保费为随机变量X.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()